使用 LLM 结合不同的响应
通用自我一致性1 旨在通过使用第二个 LLM 模型来判断个体响应的质量,从而扩展自我一致性。因此,我们不再根据每个推理链中最常出现的值来选择最终答案,而是提示模型为我们选择相对于 Prompt 最一致的答案。
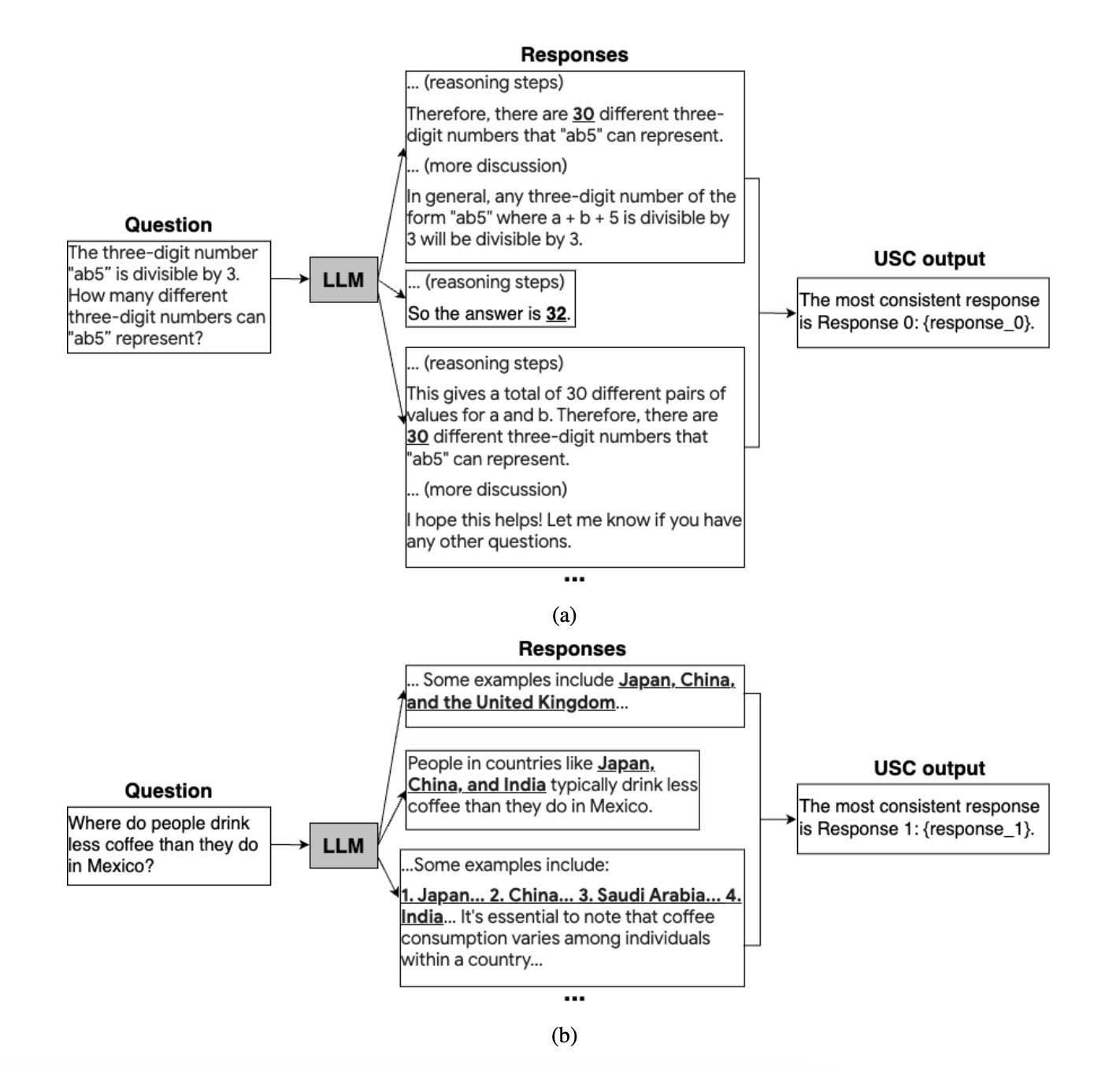
这使我们能够支持更多不同格式的响应和答案,从而带来更多样化的输出,并提高准确性。
我们可以在 instructor 中实现这一点,如下所示。
from openai import AsyncOpenAI
from pydantic import BaseModel, Field, ValidationInfo, field_validator
import instructor
from textwrap import dedent
import asyncio
client = instructor.from_openai(AsyncOpenAI())
class Response(BaseModel):
chain_of_thought: str
answer: str
class SelectedResponse(BaseModel):
most_consistent_response_id: int = Field(
description="""The ID of the most consistent response that
was provided"""
)
@field_validator("most_consistent_response_id")
@classmethod
def validate_id(cls, v: int, info: ValidationInfo):
context = info.context
number_responses = context.get("number_responses", float("inf"))
if v > number_responses:
raise ValueError(
f"""Most consistent response ID {v} is greater than the
number of responses {number_responses}. Please return a
valid id between 0 and {number_responses-1}"""
)
return v
async def generate_response(query: str) -> Response:
return await client.chat.completions.create(
model="gpt-4o",
response_model=Response,
messages=[{"role": "user", "content": query}],
)
async def generate_batch_responses(query: str, no_responses: int):
coros = [generate_response(query) for _ in range(no_responses)]
return await asyncio.gather(*coros)
async def select_consistent_response(responses: list[Response], query: str):
formatted_responses = "\n".join(
[
f"Response {idx}: {response.chain_of_thought}. {response.answer}"
for idx, response in enumerate(responses)
]
)
return await client.chat.completions.create(
model="gpt-4o",
response_model=SelectedResponse,
messages=[
{
"role": "user",
"content": dedent(
f"""
<user query>
{query}
</user query>
{formatted_responses}
Evaluate these responses.
Select the most consistent response based on majority
consensus
"""
),
}
],
validation_context={"number_responses": len(responses)},
)
if __name__ == "__main__":
query = """The three-digit number 'ab5' is divisible by 3. How many different
three-digit numbers can 'ab5' represent?"""
responses = asyncio.run(generate_batch_responses(query, 3))
for response in responses:
print(response.model_dump_json(indent=2))
"""
{
"chain_of_thought": "A number is divisible by 3 if
the sum of its digits is divisible by 3. Given the
number 'ab5', we need to check how many different
values of 'a' and 'b', where both are digits (0-9)
can make the sum divisible by 3.\n\nThe sum of the
digits is a + b + 5.\n\nWe need to find pairs (a, b)
such that (a + b + 5) % 3 == 0.",
"answer": "30"
}
"""
"""
{
"chain_of_thought": "A number is divisible by 3 if
the sum of its digits is divisible by 3. Let's
denote the digits a and b. The number 'ab5' has
digits a, b, and 5. Therefore, the sum of the
digits is a + b + 5. Since the number is divisible
by 3, a + b + 5 must be divisible by 3.\n\nNow,
since a and b are single digits (0-9), we need to
find pairs (a, b) such that a + b + 5 is divisible
by 3. We will evaluate all possible combinations of
values for a and b to count how many valid pairs
(a, b) exist.\n\nLet's start by considering b's
values:\n1. If b = 0, then a + 5 must be divisible
by 3.\n2. If b = 1, then a + 6 must be divisible by
3.\n3. If b = 2, then a + 7 must be divisible by
3.\n4. If b = 3, then a + 8 must be divisible by
3.\n5. If b = 4, then a + 9 must be divisible by
3.\n6. If b = 5, then a + 10 must be divisible by
3.\n7. If b = 6, then a + 11 must be divisible by
3.\n8. If b = 7, then a + 12 must be divisible by
3.\n9. If b = 8, then a + 13 must be divisible by
3.\n10. If b = 9, then a + 14 must be divisible by
3.\n\nWe will find all corresponding a values for
each b and count the valid combinations.\n",
"answer": "There are 30 different three-digit
numbers that 'ab5' can represent."
}
"""
"""
{
"chain_of_thought": "A number is divisible by 3 if
the sum of its digits is divisible by 3. The given
number is in the form 'ab5', where 'a' and 'b' are
digits from 0 to 9. To find the total number of
different three-digit numbers that 'ab5' can
represent, we need to determine all possible digit
combinations for 'a' and 'b' such that 'a + b + 5'
is divisible by 3.",
"answer": "30"
}
"""
selected_response = asyncio.run(select_consistent_response(responses, query))
print(selected_response.model_dump_json(indent=2))
"""
{
"most_consistent_response_id": 0
}
"""
print(
responses[selected_response.most_consistent_response_id].model_dump_json(
indent=2
)
)
"""
{
"chain_of_thought": "A number is divisible by 3 if the sum of its digits is divisible by 3. Given the number 'ab5', we need to
check how many different values of 'a' and 'b', where both are digits (0-9) can make the sum divisible by 3.\n\nThe sum of the
digits is a + b + 5.\n\nWe need to find pairs (a, b) such that (a + b + 5) % 3 == 0.",
"answer": "30"
}
"""